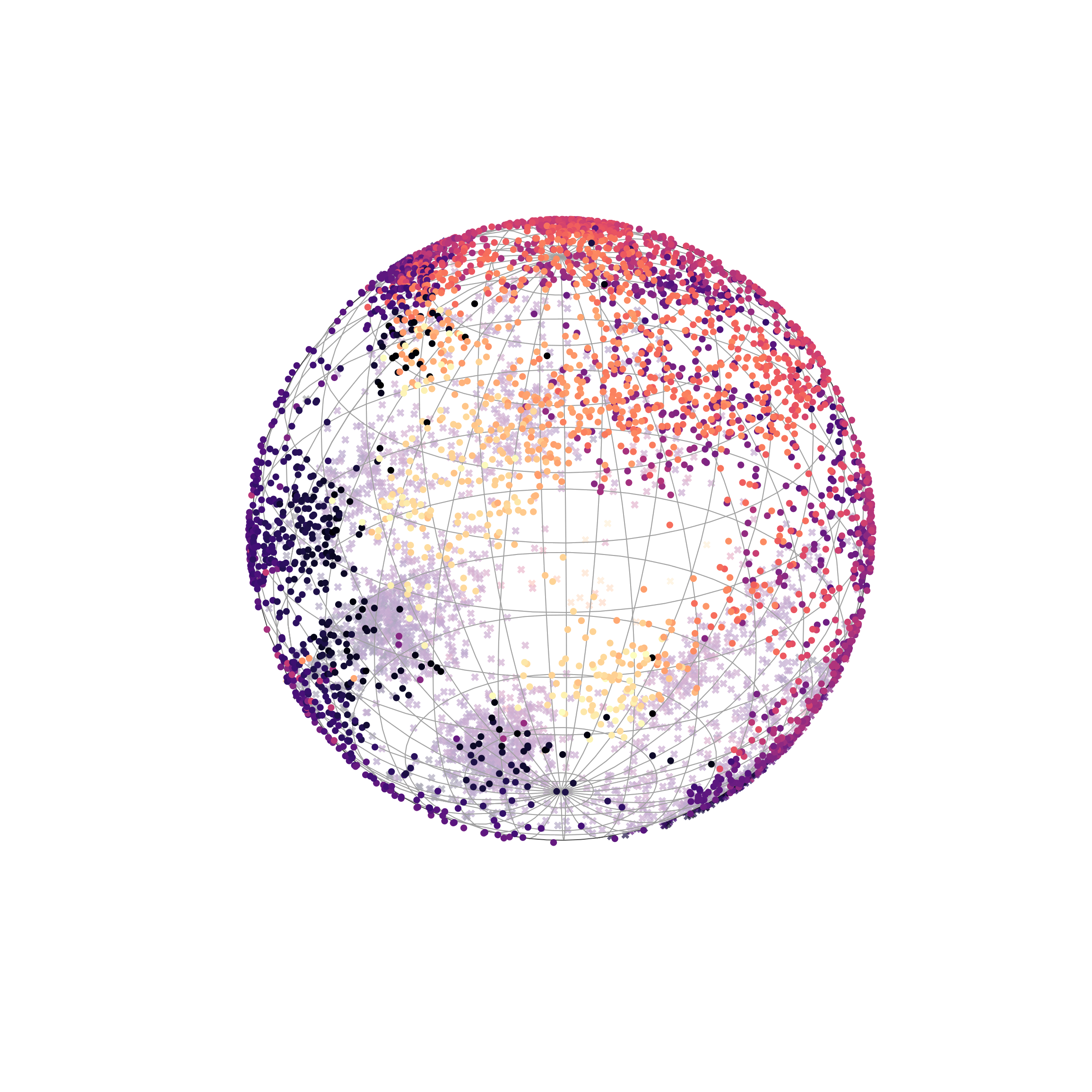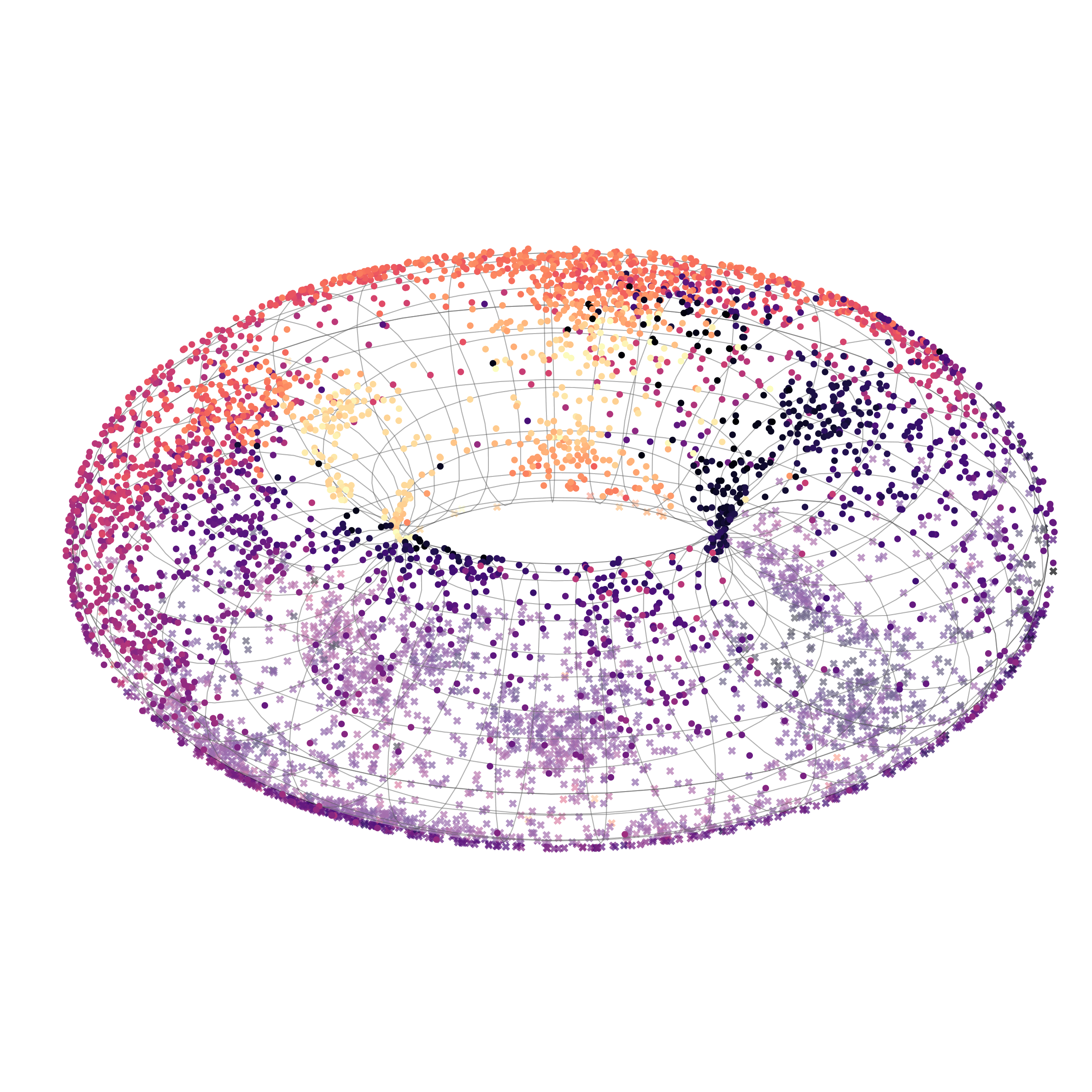Riemannian generative decoder

Simpler representation learning on manifolds. We propose a decoder-only framework to learn latents on arbitrary Riemannian manifolds via maximum likelihood and Riemannian optimization. We highlight its use with biological case studies.

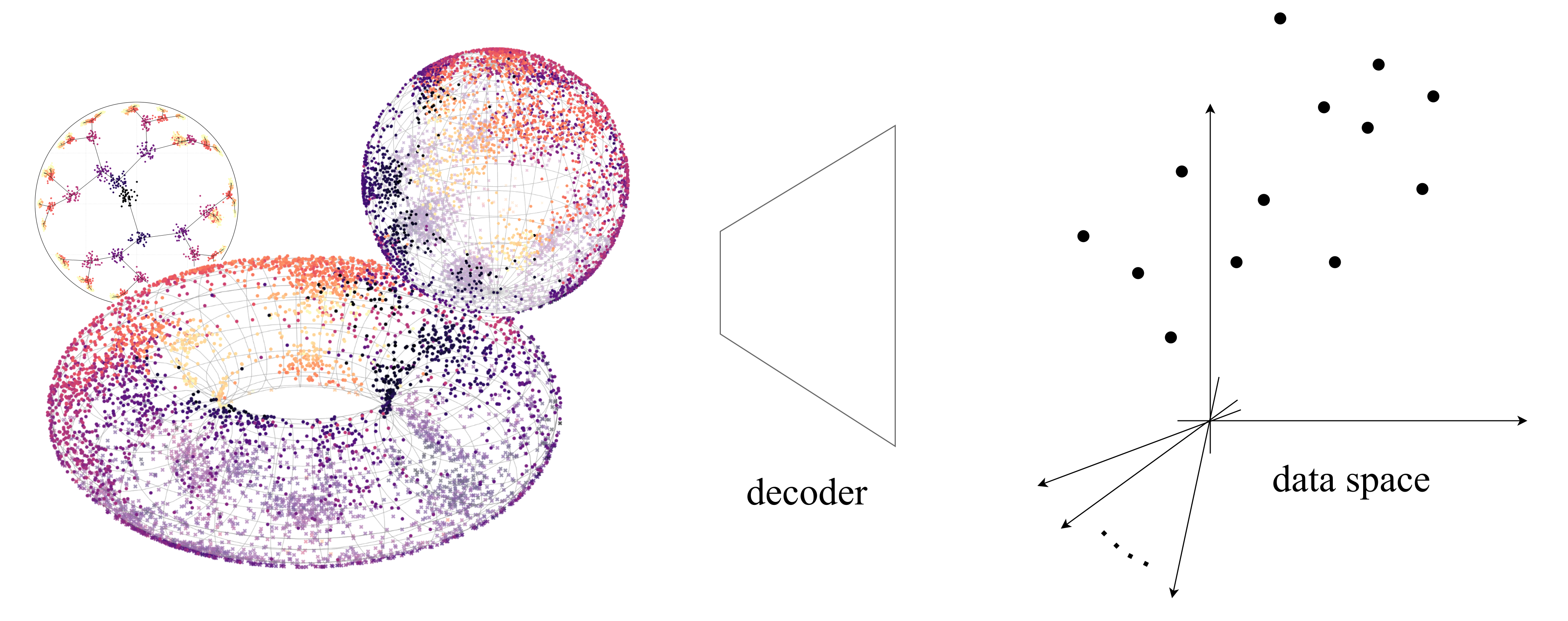
Introduction

Many datasets from biology to social sciences exhibit structures that are naturally represented by non-Euclidean geometries, such as evolutionary trees or cyclical processes. However, learning representations on manifolds usually involves complicated probabilistic approximations, potentially harming model performances. Can we simplify representation learning on manifolds by avoiding density estimation altogether?

Going encoderless circumvents density estimation

By discarding the encoder and directly learning latent variables through maximum likelihood, our method sidesteps the difficult density computations typically needed for variational inference on manifolds. Instead of the complex manifold ELBO approximations in other works, we simply directly maximize:

$ar g max_{Z, θ} \sum_{i = 1}^{N} [lo g p (x_{i} ∣ z_{i}, θ) + lo g p (z_{i})]$

where $z_{1}, z_{2}, \dots, z_{N}$ are latent representations constrained to lie on a Riemannian manifold, and $θ$ are the decoder parameters. As geoopt conveniently has gradient descent algorithms for a wide range of manifolds, choosing a manifold is as easy as swapping a single line of code. The code snippet below illustrates the basic training loop:

model.z     := init_z(n, manifold) # initialize points on a manifold
model_optim := Adam(model.decoder.parameters())
rep_optim   := RiemannianAdam([model.z])
 
for each epoch:
    rep_optim.zero_grad()
    for each (i, data) in train_loader:
        model_optim.zero_grad()
        z    := model.z[i]
        z    := add_noise(z, std, manifold) # optional regularization
        y    := model(z)
        loss := loss_fn(y, data)
        loss.backward()
        model_optim.step()
    rep_optim.step()

The GitHub codebase contains a more complete implementation.

Branching diffusions as a synthetic testbed

First, we validate our approach on synthetic data with known hierarchical structure using a branching diffusion process from this paper. This allows us to quantitatively assess how well different manifolds capture tree-like relationships.

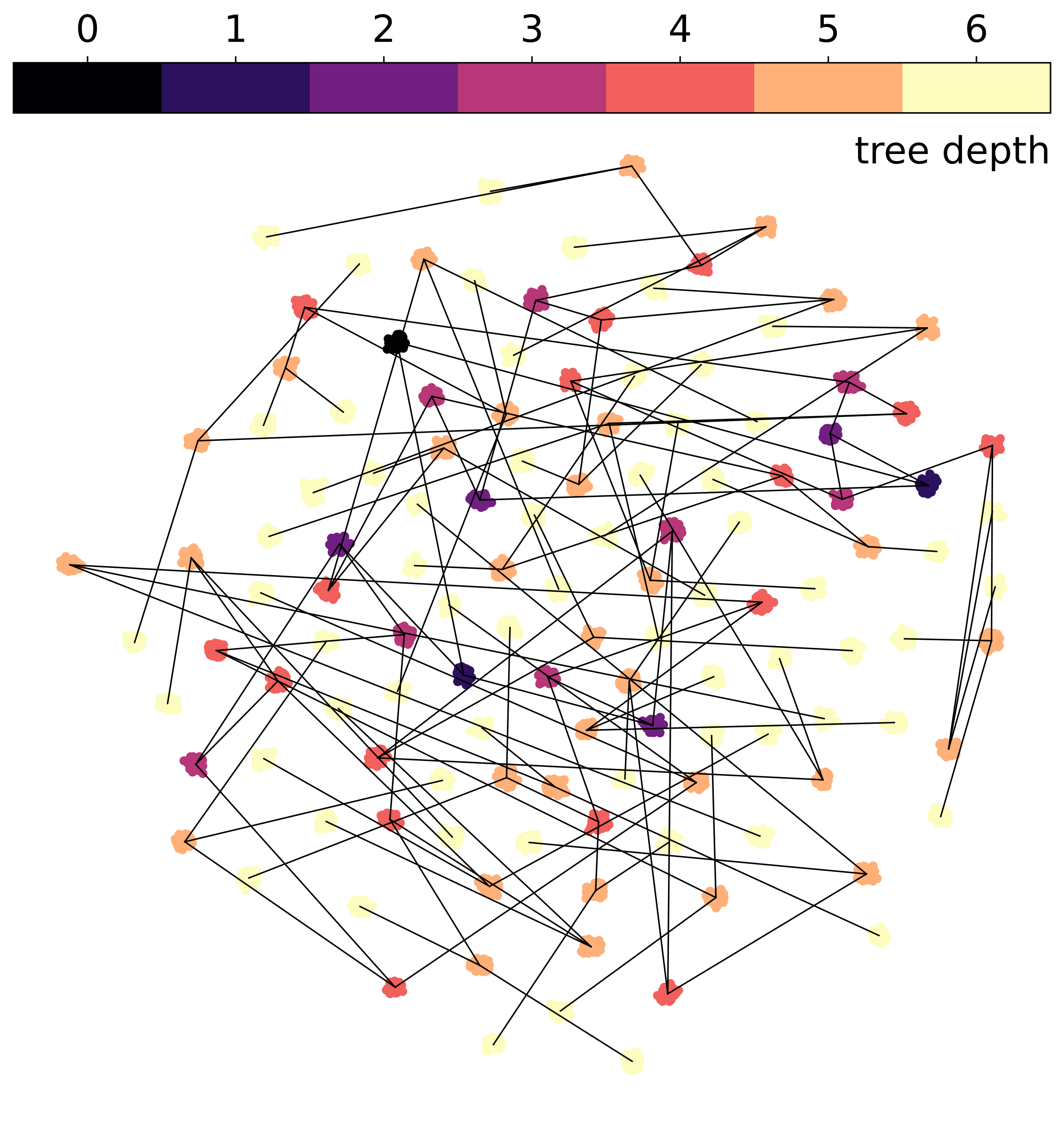
UMAP projection fails to show underlying geometry

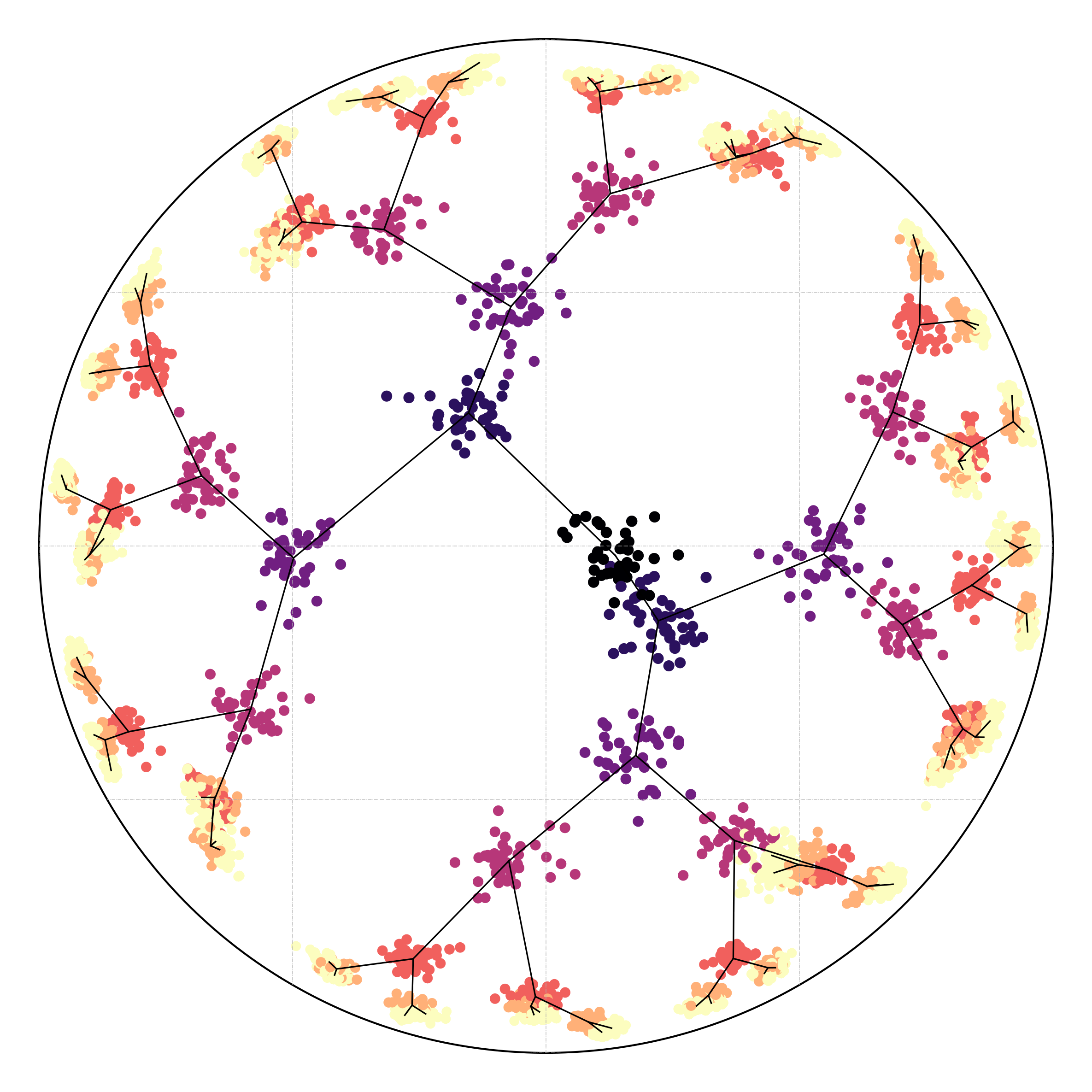
Hyperbolic (Poincaré) reveals underlying geometry

Our experiments on the synthetic data demonstrate a clear advantage of hyperbolic spaces for hierarchical data. Here, geometric regularization plays a key role in preserving the tree structure during optimization.

Geometry-aware regularization

A key innovation in our approach is geometry-aware regularization: During training, we perturb latent points by adding noise scaled according to the local curvature:

$ϵ \sim N (0, σ^{2} G^{- 1} (z))$

where $G (z)$ is the Riemannian metric tensor at point $z$ . This adapts the noise to the local curvature of the manifold — intuitively, the noise is scaled by how steep the manifold is at that point.

We found that injecting this noise results in the regularizer

$R (z) = σ^{2} Tr (J^{T} G^{- 1} (z) J)$

where $J = \nabla_{z} f_{θ} (z)$ is the decoder Jacobian. This penalizes rapid changes in output, particularly where the manifold is strongly curved.

For the Poincaré ball — a hyperbolic space — the metric is $G (z) = \frac{4}{( 1 - c ∥ z ∥ ^{2} ) ^{2}} I$ with curvature $c > 0$ . This means points further from the center receive less noise, naturally reflecting the hyperbolic geometry’s expansion toward the boundary. Our article analyzes the relationship between curvature and noise level in more detail.

An ablation study clearly shows how regularization strength $σ$ influences correlation $ρ$ between data geometry and latent geometry. The correlation improves dramatically with an increase in noise, but drops off once the noise becomes overwhelming:

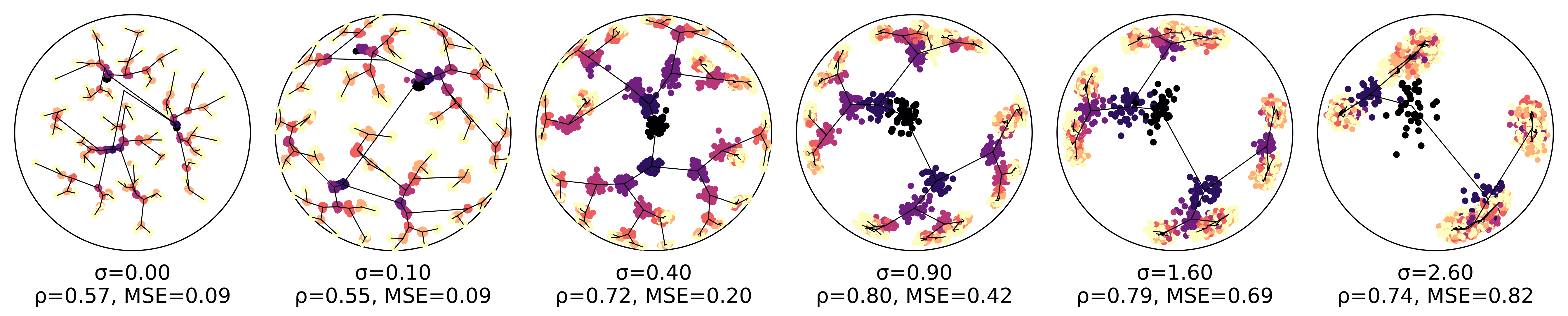
Ablation study on the effect of geometry-aware regularization.

Tracing human migrations from mtDNA

We validated our approach on mitochondrial DNA (mtDNA) sequences, which are often used to reconstruct human migration histories. mtDNA mutations form a hierarchical tree reflecting human population splits. Embedding these sequences in a hyperbolic manifold naturally captures this tree structure better than Euclidean embeddings or popular methods like UMAP.

Using hyperbolic geometry makes the inferred migrations more interpretable, highlighting branching events that match known evolutionary and geographical patterns. In the following figures, the edges represent simplified lineage relationships, with nodes indicating median haplogroup positions.

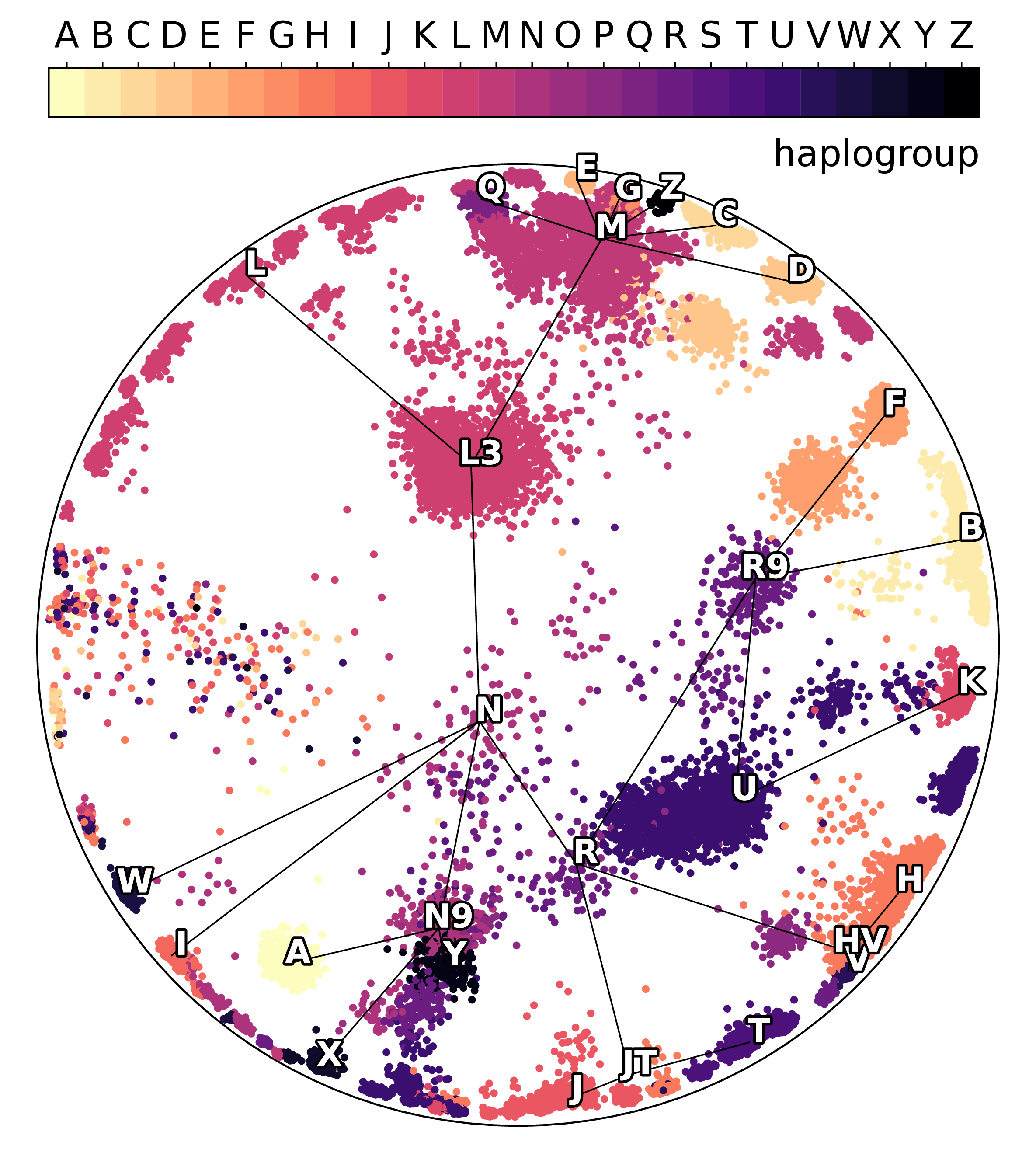
Hyperbolic latents reveal the underlying structure

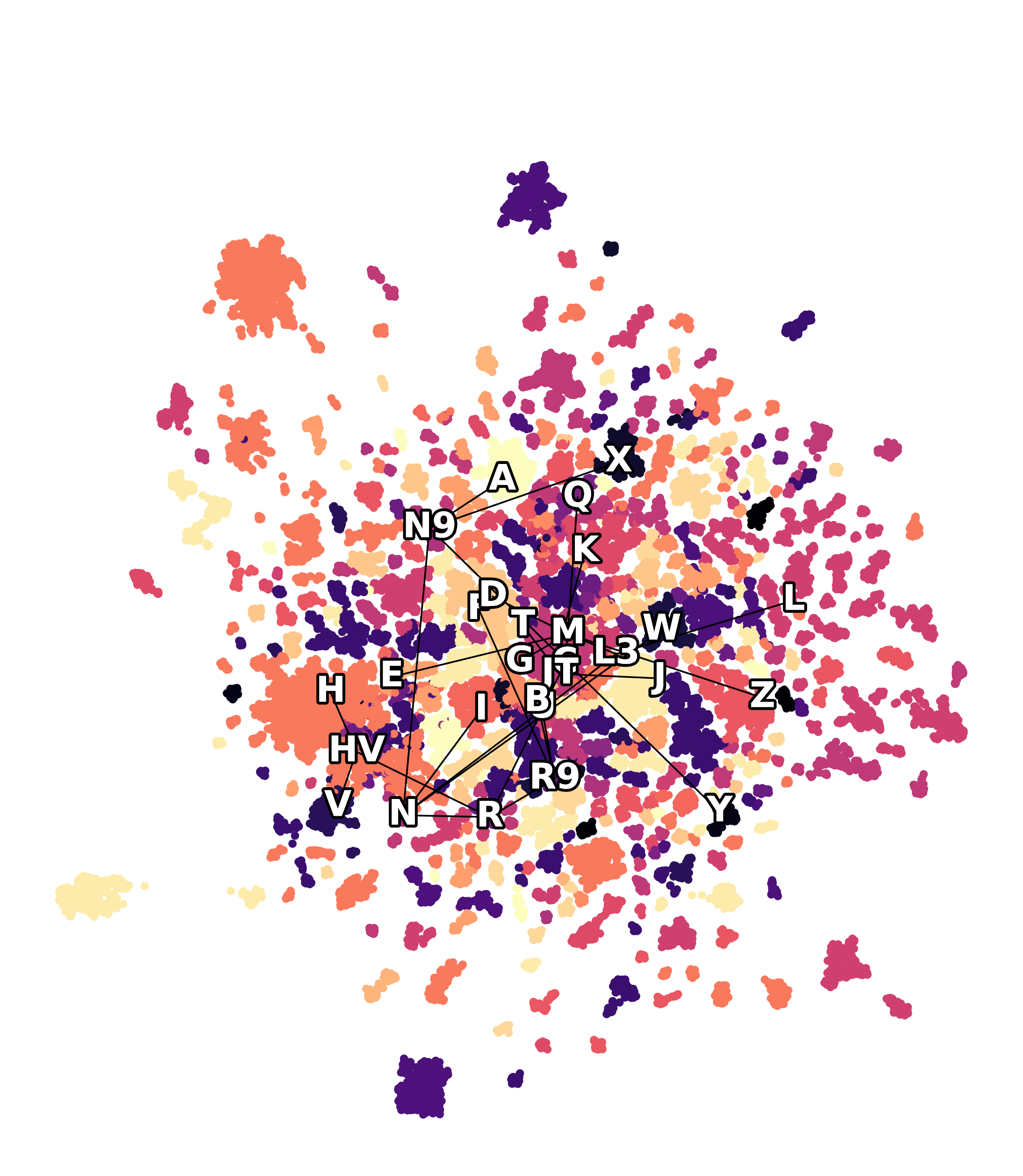
UMAP projection fails to reveal the structure

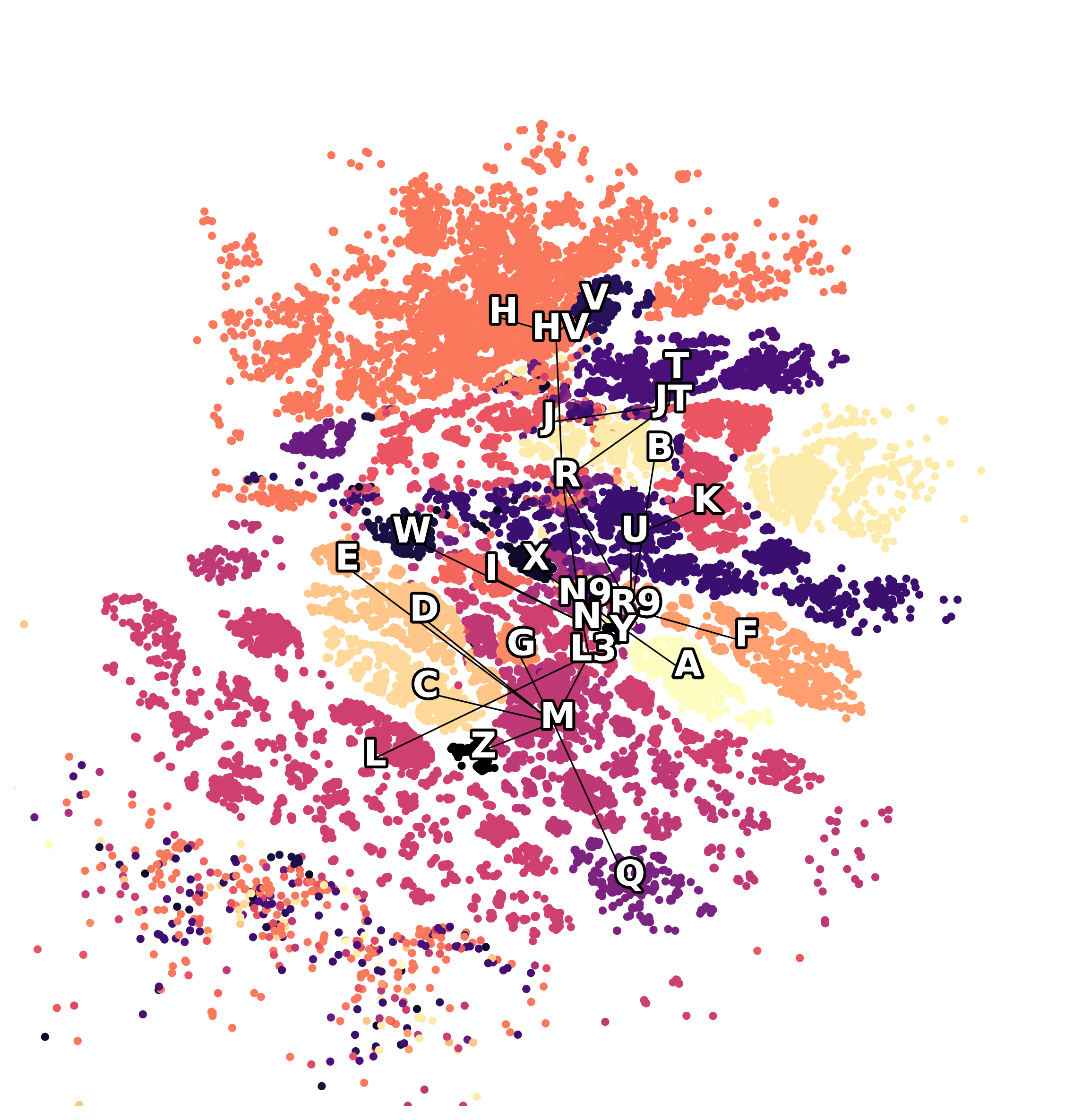
Euclidean latents show some improvement

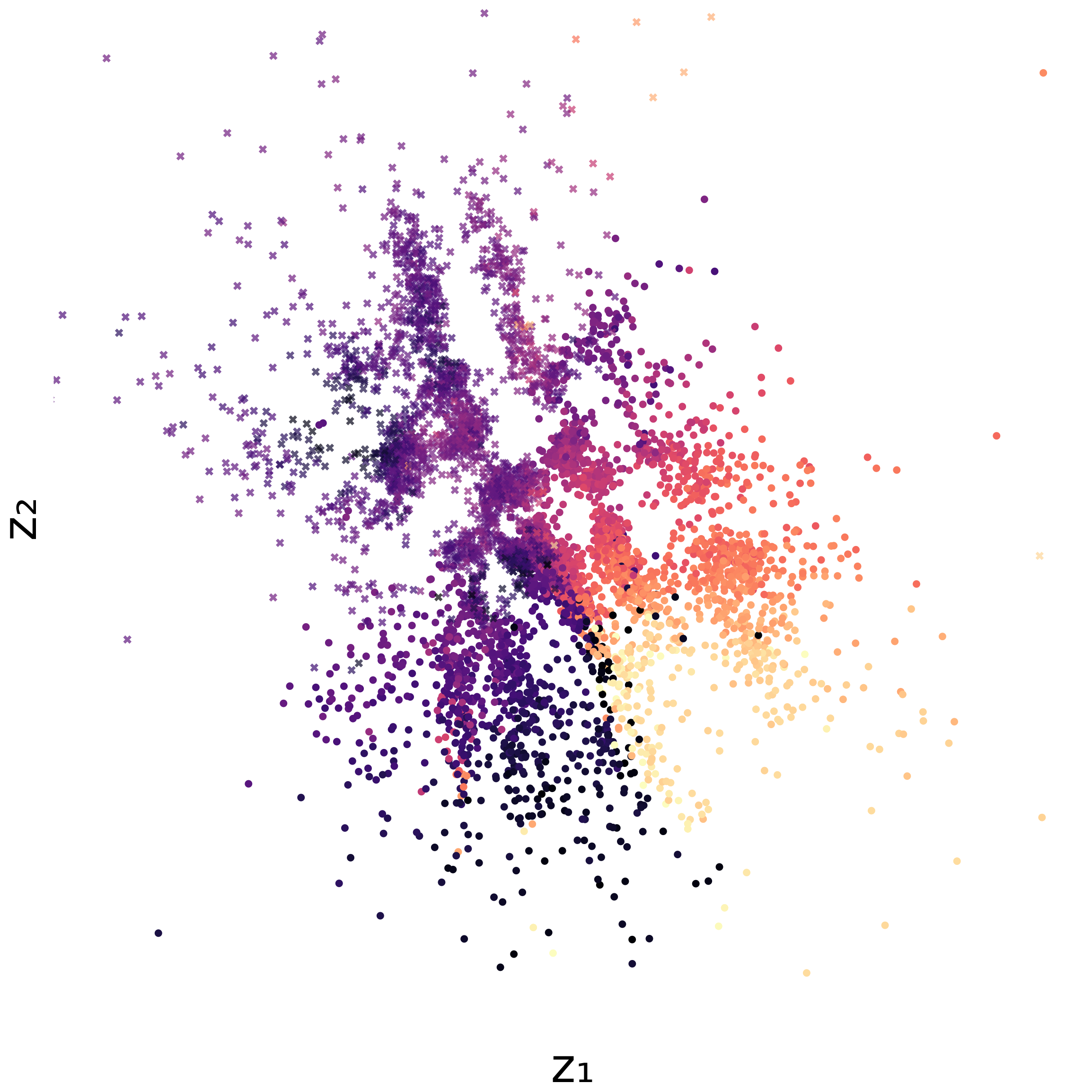
Capturing cyclical structures in single-cell data

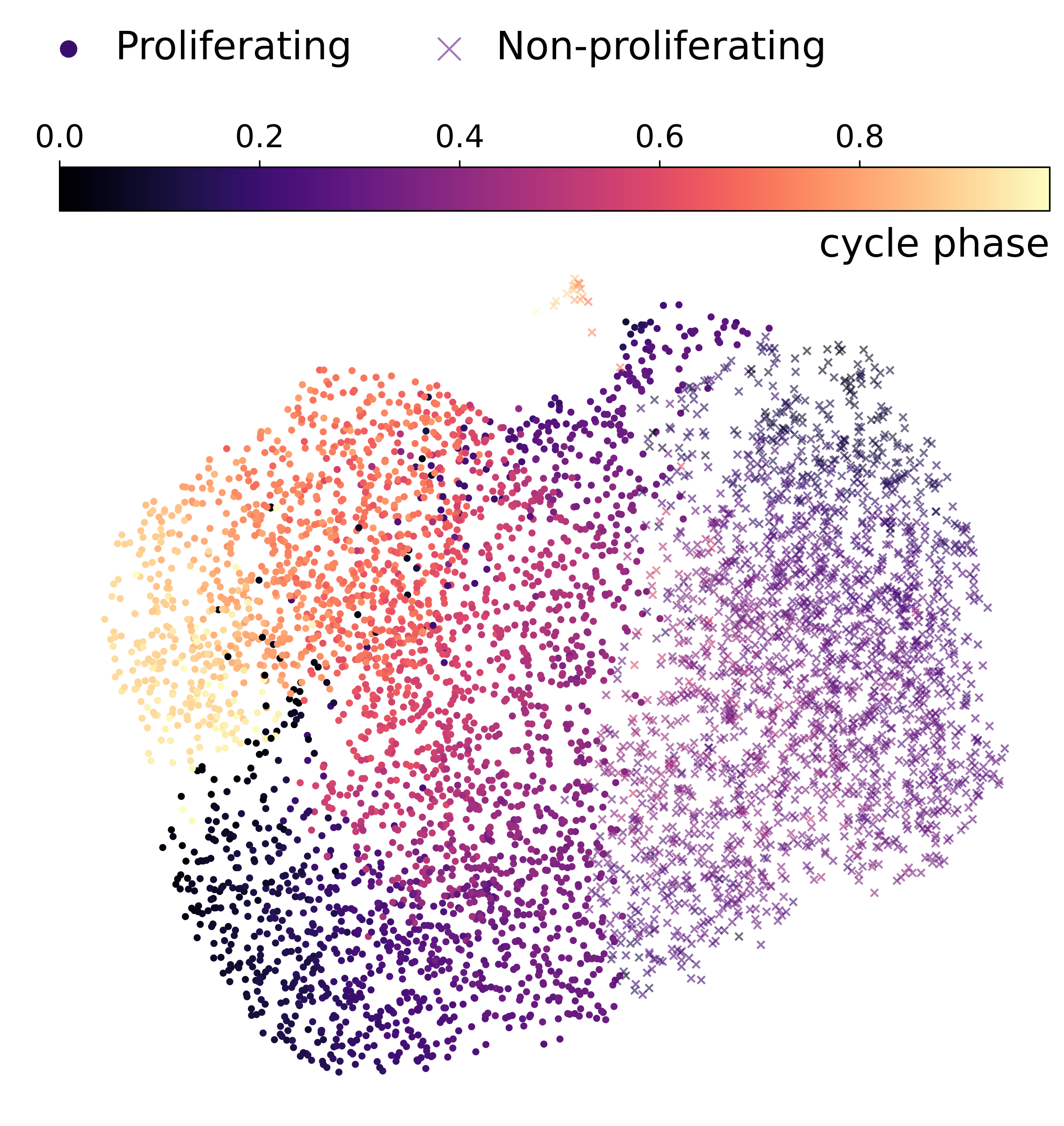
Finally, we modeled cyclic biological processes using spherical and toroidal manifolds, capturing an inherent periodicity to the data. Measuring gene expression levels of fibroblasts with single-cell RNA sequencing creates asynchronous snapshots of the cell division cycle. Since individual cells cannot be tracked over time, unsupervised learning is suitable for learning patterns about the population of cells.

Below are results using either UMAP or latents from our model:

UMAP projection of cell cycle data

Euclidean ℝ² latent space

Spherical 𝕊² latent space

Toroidal 𝕊¹×𝕊¹ latent space

Interestingly, we found that sufficiently expressive models can model the periodicity in various ways, not necessarily aligning with how humans would place them on a sphere. Nonetheless, our results still quantitatively showed that circular and toroidal embeddings improved correlation with cell cycle phase.

BibTeX

@inproceedings{bjerregaard2025riemannian,
  title={Riemannian generative decoder},
  author={Bjerregaard, Andreas and Hauberg, S{\o}ren and Krogh, Anders},
  booktitle={ICML 2025 Workshop on Generative AI and Biology},
  month     = {July},
  year      = {2025}
}

Supported manifolds

Our approach seamlessly integrates a wide variety of Riemannian manifolds provided by geoopt:

Euclidean
ProductManifold
Stiefel
CanonicalStiefel
EuclideanStiefel
EuclideanStiefelExact
Sphere
SphereExact
Stereographic
StereographicExact
PoincareBall
PoincareBallExact
SphereProjection
SphereProjectionExact
Scaled
Lorentz
SymmetricPositiveDefinite
UpperHalf
BoundedDomain

Bjerregaard's Blog

2025